Способ распределения мест по коэффициенту Бергера и Бухгольца

Если в шахматном турнире кто-то набрал одно и то же число очков, то для распределения мест используются коэффициенты Бухгольца и Бергера. Системы подсчёта применяются и в других играх, где за победу, проигрыш и ничью начисляется одинаковое число баллов: в шашках, рэндзю, Го. Ввиду такой схемы подсчёта, где нет десятых, сотых и тысячных долей, и происходят ситуации, когда количество очков у разных игроков совпадает. Коэффициенты немного отличаются и используются в разных турнирах. Преподаватели онлайн-школы шахмат «ТАКТИКУМ» предлагают вместе разобраться, в каких случаях их применяют и как рассчитывают.

Коэффициент Бергера применим в соревнованиях, проходящих по круговому принципу, то есть в тех, где каждый участник в турах играет партию с каждым. Это популярный способ организации соревнований в настольных логических играх, включая шахматы. Для определения очерёдности того, кто с кем будет играть, используются специальные таблицы, которые, как и рассматриваемый коэффициент, называют таблицами Бергера.

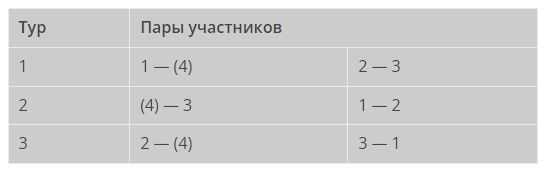
Пример одной из таблиц для кругового турнира 3 или 4 участников представлен на изображении ниже. При нечётном количестве участников цифра в первом столбике вне скобок указывает на участника, который свободен от игры в данном туре. То есть если их 3, то в первом туре 1-й участник отдыхает, поскольку 4-го игрока нет. Аналогично во втором и третьем туре не играет 3-й и 2-й участник соответственно.

В таких турнирах при необходимости и рассчитывают коэффициент Бергера. Впервые его использовали в Ливерпуле в 1882 году, а через 4 года стали практиковать систему распределения мест регулярно. Разберём, как в шахматах считать коэффициент Бергера. Удобнее представить порядок расчёта в виде формулы:

КБ = Сп + 0,5⸱Сн.

Что означают символы в формуле:

Получается из игроков с одним числом очков побеждает тот, чьи соперники (проигравшие и сыгравшие вничью) играли лучше, т. е. набрали в турах с конкретным участником больше баллов. Такая система подсчёта может использоваться не только в круговых турнирах, но и в тех, что организованы по швейцарской системе. Но чаще всего для них обычно рассчитывают уже коэффициент Бухгольца.

С помощью коэффициента Бухгольца в шахматах тоже определяют победителя среди тех, кто набрал одинаковое число очков. Но система стала использоваться позже предыдущей, в 1932 году, и, как было сказано выше, она предназначена для соревнований, организуемых по швейцарской системе. Обычно это турниры с очень большим количеством участников, как детей, так и взрослых.

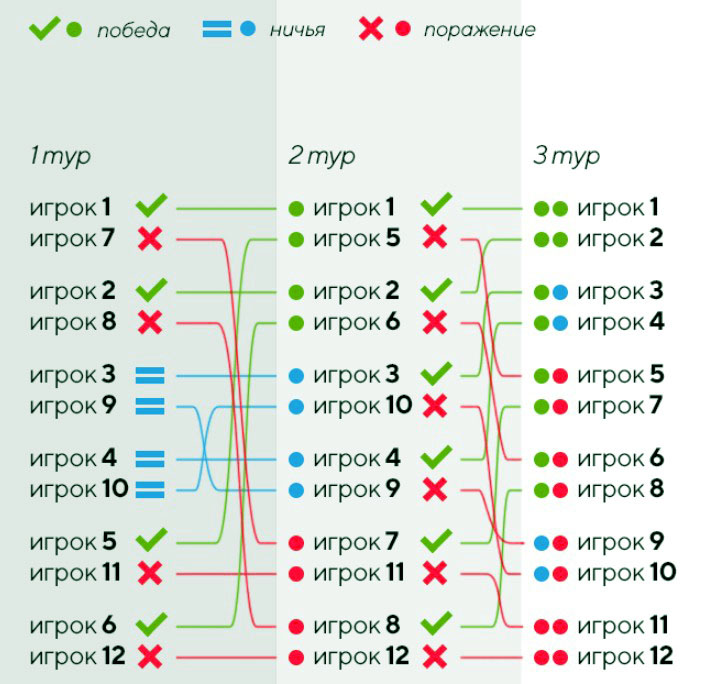
В первом туре соперников выбирают путем жеребьёвки из всех сразу или из категорий участников, упорядоченных и разделённых на группы по рейтингу. Со второго тура выбирают уже среди тех, у кого одинаковое количество очков: победители играют с победителями, а проигравшие — с проигравшими. И так до конца самого турнира, без выбываний. В соответствии с набранными очками распределяются места, а если есть те, у кого их поровну, то используется коэффициент Бухгольца.

Говоря о том, как в шахматах считать коэффициент Бухгольца, нужно отметить, что здесь суммируются уже все очки соперников участника. То есть не имеет значения результат встречи. Суть системы распределения заключается в том, что игрок тем сильнее, чем сильнее были все его соперники, а не только те, кого он обыграл и с кем была ничья. В виде формулы это будет выглядеть так:

КБ1 = Св.

Расшифровка обозначений в формуле:

У кого из участников с одними баллами итоговое число получится больше, тот и становится лучшим. Если и вы хотите побеждать в соревнованиях по шахматам, причём уверенно, а не только по дополнительным подсчётам — рекомендуем записаться на индивидуальные занятия, в рамках которых опытный преподаватель на основе оценки уровня подготовки составит персональный план обучения и поможет добиться поставленной цели.

Стоит отметить, что в способе распределения коэффициента и Бергера, и Бухгольца несыгранные партии приравниваются к ничейным. Речь идёт о пропуске тура, неявке, нехватке соперника:

Это даёт возможность сопоставлять уровень игроков с разным числом партий и позволяет оценивать их более справедливо. Если не учитывать пропущенные туры в расчётах, то может получиться так, что участник будет иметь заведомо более низкие коэффициенты, хотя его вины в этом нет, а причина в том, что соперник отсутствовал или не явился. Для компенсации и начисляются очки Бухгольца или Бергера, т. е. накидываются те самые условные «половинки» , что помогает исключить нелогичные провалы коэффициентов из-за несыгранных партий.

Теги: шахматы, термины, турнир, очки, баллы